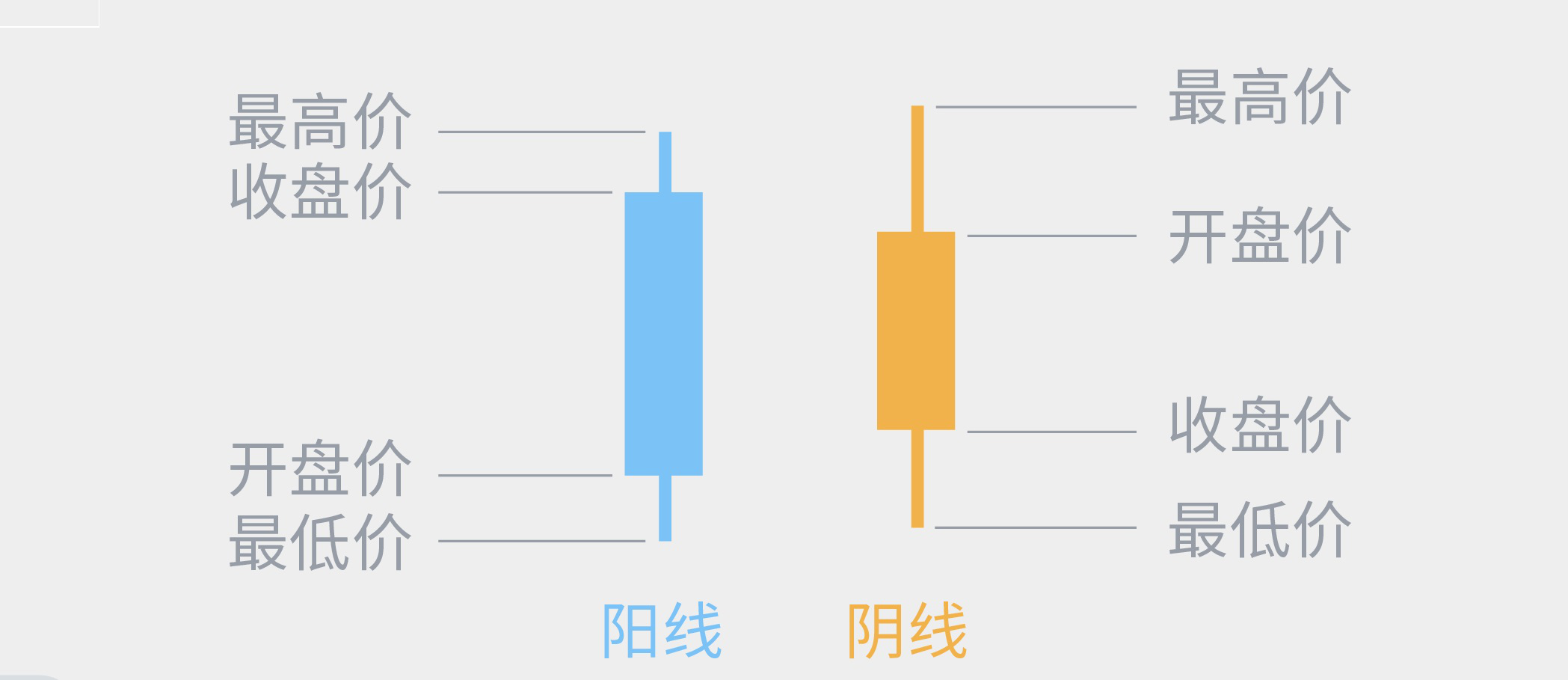
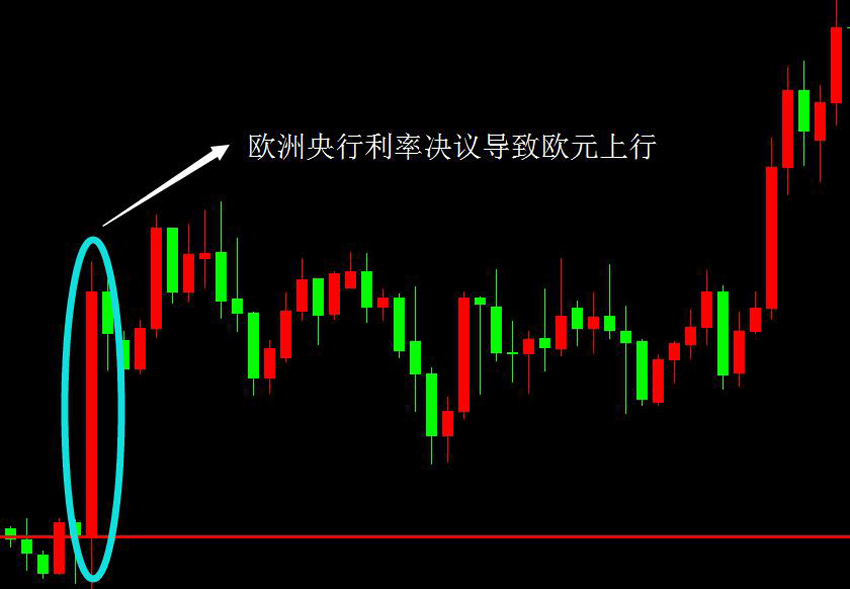
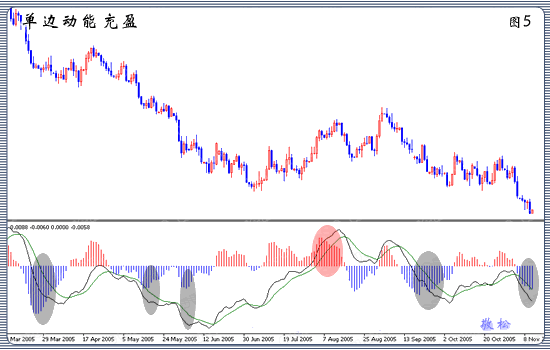
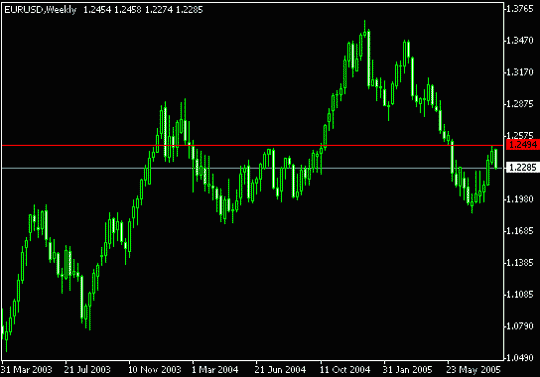
正如埃利奥特本人所承认的,他理论的基础是数的序列,这是由巨大的意大利数学家早在13世纪就发现的。
比萨商人列昂纳多(1180~1240年),其更为人知的名字是绰号斐波那契,无疑是中世纪最紧张的数学家。他的著尴尬刁难数学学科的发展和欧洲数学知识的传播起到不可估量的紧张作用。列昂纳多的生活和学术生涯与欧洲科学文化的发展紧密相连。
斐波那契时代距文艺中兴还很迢遥,但历史却慷慨地赠予意大利一段美妙的时间,完全可以称之为即将到来的文艺中兴时期的预演。这一预演是由腓特烈二世向导的,自1220年起,他是神圣罗马帝国的皇帝。腓特烈二世深受南意大利传统的陶冶,与欧洲的基督教王国极其疏远。
例如,腓特烈二世对深为他祖父所钟爱的军事比武没有涓滴爱好。战争之后还提什么保持几个世纪以来的传统呢!分外是当你回忆起,他不好比武而推广更少血腥的数学竞赛,竞争的对手不再互相拳打脚踢而是互相出数学题。真是一个怪人,不是吗?
斐波那契老师出人头地的时刻就在这些数学比武中到来了。正是在比武场上他那毋庸置疑的才华得到充分光显的展示。当然,这是得益于他的父亲商人波那契给儿子的优秀教育。这位商人本身带着儿子来到东方,并且把儿子送到阿拉伯先生那里。您大概记得,当时东方人文化程度很高(即进化得更好),分外是在数学方面。因此,列昂纳多所接受的是最好的教育,当时最先辈的教育。
有了如许的教育再加上腓特烈的鼓励政策,斐波那契的学术论文当然得以面世。天然,斐波那契的著作得到腓特烈二世的赏识……噢,老师,国王可是一张大王牌。
大王如此紧张,教育如此优秀,因此,斐波那契一会儿就有三部宏篇巨著问世。其中最闻名、流传最广的一部叫作《Liber Abaci》。正是因为有了这部书,欧洲才知晓了印度和阿拉伯计数系统,后来这种系统庖代了当时传统的罗马数字。斐波那契的著尴尬刁难此后数学、物理、天文和技术的发展都起到了紧张作用。总而言之,斐波那契对那里的作用就相称于祖冲之对于中国。
在《Liber Abaci》中到底有什么超天然的东西呢?斐波那契的独到之处在于适用于兔子的公式(确切地说,是其滋生过程)。没错没错,这里说的就是兔子,白白的,毛茸茸的,人见人爱的兔子。在兔子滋生的语境中斐波那契举出本身的数列作为对一个数学题目的解答,这个题目就是找到兔子滋生的公式。原始数据再简单不过:先在一个笼子里放一只雄兔,然后再放一只雌兔,如今共有两只兔子;然后我们就可以歇息了,这两个小动物会自力进行操作,经过肯定的幸福兔子之夜后,世界上就会出现斐波那契数列中的那个数。
斐波那契的数列是如许的:1,1,2,3,5,8,13,21,34,55,89,144(直至无穷)。斐波那契数列不仅仅是一大堆数字而已,它有着特别很是风趣的特征:这些数字之间彼此有着恒
定的关系。这种关系如下:
任意两个邻数的和都等于数列中的下一个数。例如:3+5=8;5+8=13等等。
数列中的任意一个数与下一个数的比值都渐渐接近0.618。
例如:
1∶1=1
1∶2=0.5
2∶3=0.67
3∶5=0.6
5∶8=0.625
8∶13=0.615
13∶21=0.619 等等。
请细致,比值是在0.618四周摇荡,而且摆动范围渐渐减小。为了避免误入邪路,我们如今要明确一下,所谓的摆动范围可不是指幅长,而是围绕”中线”的摆动幅度。简而言之,有报价,也有报价与中心值之间的误差。个别的报价增长或削减通常没有任何清晰的规律性,至多是有某种模糊的假设。于是人们决定发明出一点确定的东西,决定把这些围绕中心值自觉的摇荡称为摆动,并且分析所谓的活动无序程度。
任意一个数与前一个数的比值都近似于1.618(这是0.618的逆数)。如:
13∶8=1.625
21∶13=1.615
34∶21=1.619。
这两个数越大,其比值越接近0.618和1.618。
任意一个数与厥后面隔一个数的比值都接近0.382,而与前面隔一个数的比值接近2.618。例如:
13∶34=0.382
34∶13=2.615等。
斐波那契数列还包含着另外一些风趣的关系(系数)。但我们上面所列举的这些最为紧张,也最为闻名。
现实上斐波那契并不是这些比值的第一发明者。由于系数1.618或者0.618早在古希腊和古埃及的数学中就已出现。它们被称为”黄金系数”或”黄金分割”。音乐、造型艺术、建筑、生物等学科中都可以看到它的身影。例如,古希腊人运用”黄金分割”原则建的帕耳忒农庙,古埃及人用同样的方法在吉萨建了巨大的金字塔。而且,毕达哥拉斯、柏拉图和列昂纳多·达·芬奇都特别很是了解”黄金系数”的特点。总之,许多受人尊敬的老师们都知道这两个有魔力的数字。于是就产生一个题目:这两个数字会不会对我们也有效呢?假如答案是一定的,又该如何行使这个巨大的发现呢?
它们有效!它们用起来也很简单!
斐波那契的比例不仅提供了回撤的可能水平,而且指出趋势持续情况下冲程的可能值。假如经过冲程后市场后退,而此后持续朝统一方向活动,那么在典型的情景中持续冲程值可能达1.618。